| You Are Not Logged In | Login/Get New Account |
|
Please Log In. Accounts are free!
Logged In users are granted additional features including a more current version of the Archives and a simplified process for submitting articles. |
|
MMD
 Gallery
Gallery
 Tech
Tech
 AM&FM
AM&FM
|
|
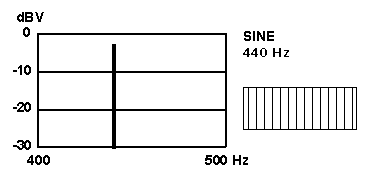
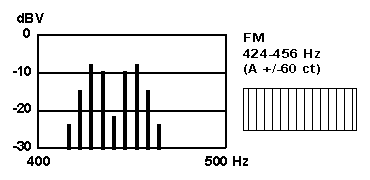
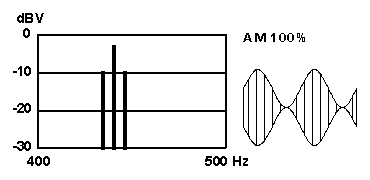
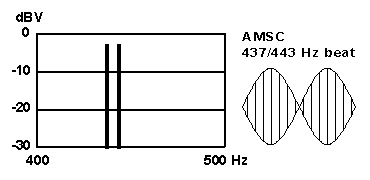
A sustained discussion thread about the musical terms tremolo and vibrato developed in MMDigest in October 1999 [ ref. http://www.mmdigest.com/Archives/KWIC/T/tremolo.html ]. These terms allude to the quavering sound produced by a skilled violinist or singer, and also to the "effects" devices which can be applied to modify the sound of a pipe organ or modern electronic organ or synthesizer. In the case when the underlying tone is a sinusoidal waveform, or sinewave, the result of applying tremolo or vibrato modulation is easily described with simple equations and demonstrated with common laboratory equipment such as the audio oscillator and oscilloscope. Since the terms tremolo and vibrato are not rigorously defined by the musical world, engineers call the effects AM and FM, meaning amplitude modulation and frequency modulation. The underlying unvarying tone is called the carrier frequency, and how fast the amplitude/frequency is undulated is the modulation frequency. These precise terms (and the descriptive equations) come from telephone and radio technology. A musical instrument that features amplitude modulation (AM) is the Deagan Vibraphone, a sort of marimba with motor-driven rotating shutters that vary the sound amplitude. The steel guitar (or Hawaiian guitar) features frequency modulation (FM) as the player wiggles the heavy steel bar back and forth to vary the speaking length of the vibrating string. To illustrate what different modulation forms sound like I have fabricated four synthetic auditory demonstration files. They all share these common parameters: duration: 1 second
The basic signal, or carrier, is a pure sinusoid, so that the samples are devoid of any timbral character that would associate them with any real instrument. Instead, they are intended to point at the specific character evoked by the tremolo/vibrato or AM/FM in itself. The figures below show the power spectrum (energy versus frequency) and the waveform envelope as would be seen on an oscilloscope (amplitude versus time). Click on the underlined WAV-file name or the picture and the browser
should launch a system program at your computer which will play the 1-second
sound via the computers sound card and loudspeaker. Then use the
"Back" button to return to this text page.
99-10-21 19:50 +0100 |
|
|
|
|
|
|
|
|
|
CONTACT FORM: Click HERE to write to the editor, or to post a message about Mechanical Musical Instruments to the MMD Unless otherwise noted, all opinions are those of the individual authors and may not represent those of the editors. Compilation copyright 1995-2025 by Jody Kravitz. Please read our Republication Policy before copying information from or creating links to this web site. Click HERE to contact the webmaster regarding problems with the website. |
|
|
||||||
|