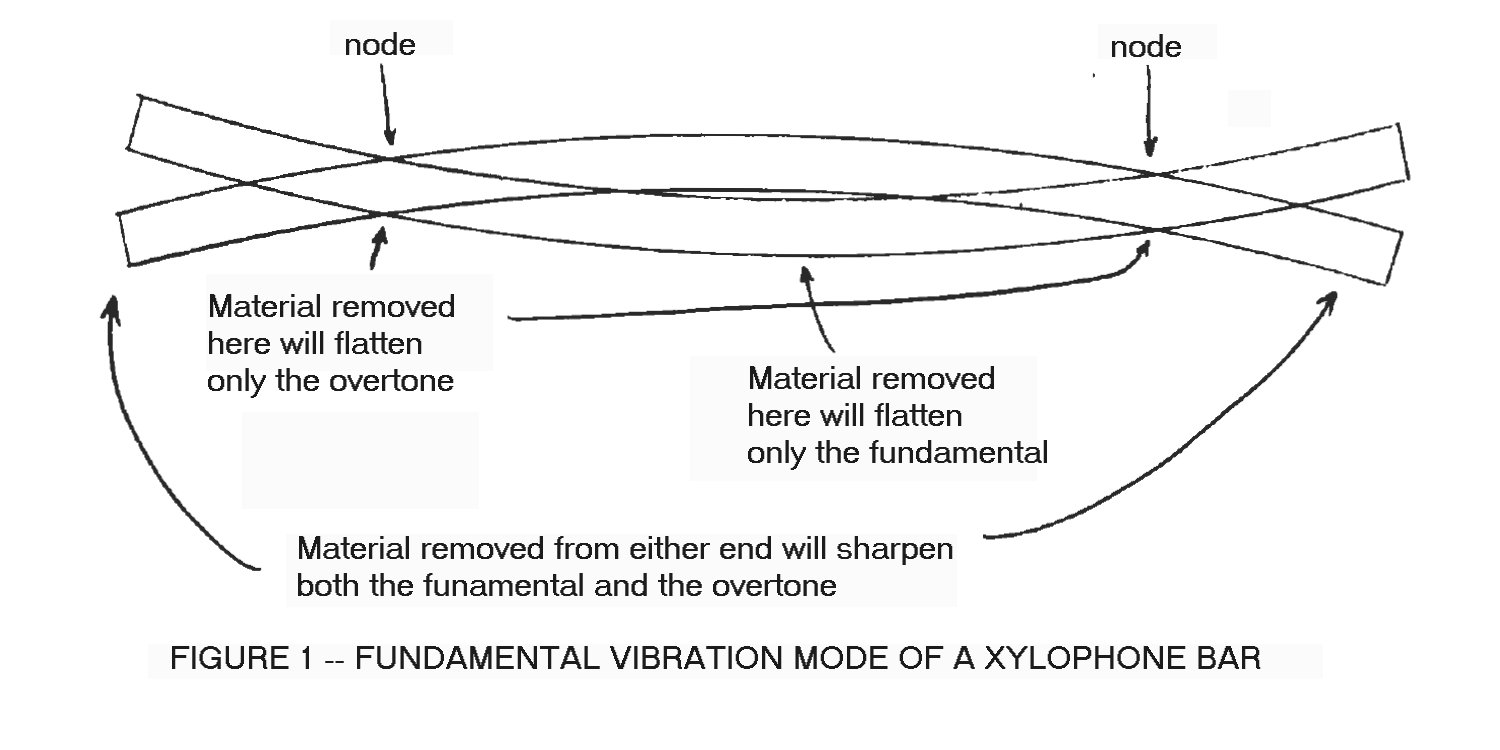
All of the above-mentioned instruments (including church-type chimes) share one common characteristic which makes them quite different from most other instruments: their tone bars vibrate in much the same way that other percussion instruments do (such as piano, guitar, etc.), except that their stiffness is the dominant pitch-determining characteristic instead of the tension they are subject to, as in piano and guitar strings. This gives them a set of natural overtones that are distinctly different from those of other instruments. It is this same "stiffness" that gives rise to "stretching of the octaves" in the upper and lower registers of piano tuning.

Specifically, most tone-producing instruments (violin, organ pipes, brass and woodwind instruments, etc.) generate a set of overtones, which are higher pitches in addition to the basic fundamental tone, and whose frequencies are exact integral multiples of the fundamental tone. They are known as "harmonics", both in musical and electronic engineering circles, and it is fairly safe to use the terms "overtone" and "harmonic" interchangeably, until you get to vibrating devices whose stiffness becomes significant. Our whole system of harmony, keyboard layout, musical chords, and musical composition is predicated on the fact that most musical instruments have a series of overtones that are also harmonics. For example, middle C, as a fundamental tone, has overtone (or harmonics) whose pitches correspond to C (one octave above), G (1-1/2 octaves above), C (2 octaves above), E (2-1/3 octaves above), G (2-1/2 octaves above), C (3 octaves above), ad infinitum. These correspond to the second, third, fourth, fifth, sixth, and eighth harmonics. As many as twenty of these harmonics can be significant in establishing the tone character, or timbre, of a tone.

This is where vibrating bars differ, musically and physically, from vibrating string or vibrating air-column instruments. A vibrating bar has a series of overtones which are definitely not harmonics; that is, the pitches of these overtones are not integral multiples of the fundamental pitch. It is precisely this non-harmonicity that gives these vibrating bars their distinctive tone. Specifically, for a bar of uniform cross-section (that is, one which has not been "undercut"), the middle C bar will have overtones whose pitches correspond approximately to F# (1-1/2 octaves above), and a series of higher ones which are of lesser importance (except for church chimes -- more on that later).

This order of overtone structure will prevail regardless of the length, width, thickness, or type of material from which the bar is made (metal, wood, etc.), although the fundamental pitch will be strongly affected by all the above factors except width. In particular, the frequency of vibration of a bar of uniform cross-section is proportional directly to its thickness, and inversely to the square of its length. That is, if a bar were ground to half its original thickness, its pitch would be halved (i.e., lowered one octave). Further, if a bar were cut to half its original length, its pitch would be quadrupled (i.e., raised two octaves). Thus, such a bar can be tuned by grinding away small amounts of material on its ends or in its thickness, depending on whether it needs to be sharped or flatted, respectively. To a limited extent an unintentional "overshooting" of one can be compensated by the other. To raise the pitch of a bar by one semitone, you would need to remove about 3 percent of its length.

Instruments which have bars that have more or less uniform cross-section are orchestra bells, glockenspiel and xylophone. Instruments which have intentionally non-uniform bars include vibraphone, organ harp, celesta and marimba; these latter instruments have bars that are deeply undercut near the center, giving them a particularly mellow tone due to the resulting overtone structure. A further constraint that the instrument designer (or restorer) must work within is that, for the sake of appearance, a set of bars must gradually taper in length from one end to the other. If a new set is being constructed, this will come about naturally if all bars are made the same thickness and out of the same material (whether wood or metal). However, if you find yourself needing to make one or two bars to complete a set, some experimentation will be necessary. Generally, the shortest bar of a two octave set, say, will be about half the length of the longest bar.

Probably one of the more interesting facets of the design of a vibrating bar, or set of bars, is that the fundamental tone and the first overtone of a bar are each separately tunable and, in fact, they both must be tuned. The pitch of the overtone is very nearly as important as the pitch of the fundamental tone, although not quite as critical. As stated above, the first overtone of a uniform bar will naturally occur at about 18 semitones (or about 1-1/2 octaves) above the fundamental pitch. This particular interval happens to be somewhat dissonant when played in chords with other instruments, but it gives the xylophone its characteristic "plink" type of sound, and is usually satisfactory. Orchestra bells fall into the same category. The tubular resonators which are often used under the bars on a xylophone serve to amplify the fundamental tone, and to a minor extent, the first overtone.

If the interval between fundamental and first overtone pitches is the same (say, 18 semitones) for all the bars in a set, then the apparent tone quality will be consistent from top to bottom, and the slight dissonance will be quite satisfactory to the ear.

Figure 1 shows a typical bar and the method of tuning the fundamental tone and the overtone, separately and together. Notice that material removed from the ends of the bar will cause both the fundamental and the overtone to rise in pitch, whereas material removed from the center will flatten only the fundamental, and material removed near the nodes (about 25% inward from each end) will flatten only the overtone. It is in this way that the fundamental and the overtone are separately tunable, and it is very important when tuning to remove material from the proper areas in order to obtain the desired result.

Since material removed from the center area will flatten the fundamental tone only, the spread between the two tones will thereby be broadened (say to 19 or more semitones). In particular, if enough material is removed from the center area to broaden the interval to 24 semitones, which is exactly two octaves, then the combination will be very pleasing (somewhat mellow) to the ear. This is the case with marimba, organ harp and vibraphone bars. The tubular resonators used under these bars serve to amplify only the fundamental tone, further mellowing the tone. This, then, is the reason that the bars on these instruments always are very deeply undercut.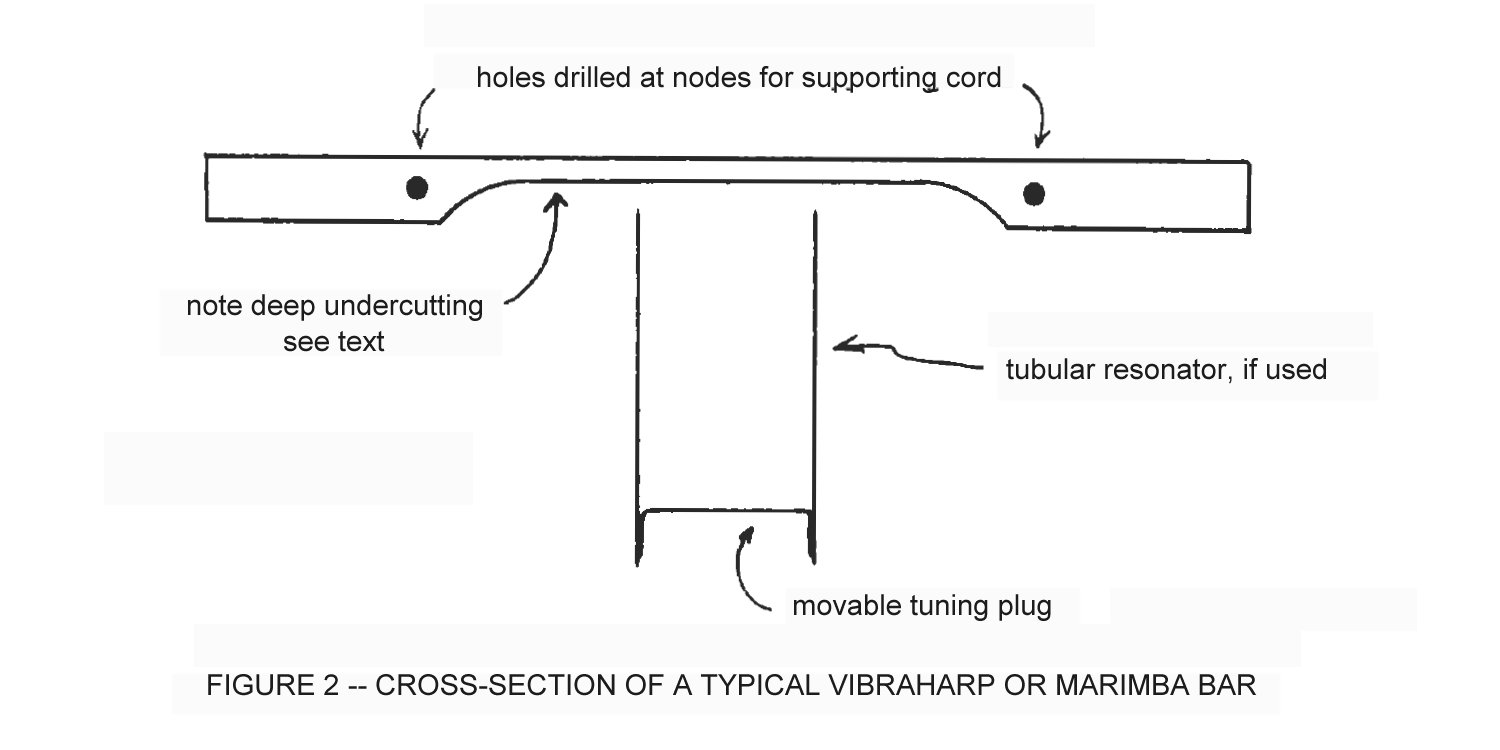

Actually, when tuning the overtone, material should be removed not exactly at the node position, but from an area slightly toward the center of the bar from the node, particularly in the case of cord-type support. Since a hole will be drilled at the node, any further removal of material at the surface will weaken the mechanical strength of the bar.

When tuning the bar, either overtone or fundamental, material could be removed merely by cutting part way through the bar, in the appropriate place, with a saw blade. However, commercial manufacturers cut away material from a broader area, apparently using a drum-type sander. Most likely the reason is that the resultant bending during vibration of the bar will be distributed over a larger area, lessening the likelihood of material fatigue at that point. In any event, the appearance is certainly more appealing with the gradual curve.

As for actually tuning to final pitch, some pitch reference will be necessary, such as a piano, organ, or electronic tuning device, unless the tuner happens to be blessed with absolute pitch. Certainly some degree of relative pitch development would be desirable, since the overtone and the fundamental tone must be separately distinguished, each in the presence of the other. The fundamental can be excited alone by carefully striking the bar exactly in its center; the overtone can be excited alone by striking the bar exactly at one of the nodes. However, such a procedure is more useful in identifying the pitch of the overtone in the mind of the listener than in actual practical tuning.

As for selection of materials, some experimentation is in order here also. For metal bars, common aluminum alloys such as 6061 can be used, in thicknesses from 1/8 inch to perhaps 1/2 inch, depending on whether an existing set is being matched or a new set is being constructed. The width of each bar should be at least twice its thickness. Wood bars should be made of a dense hardwood, preferably rosewood, but walnut, maple, or other hardwood can be used. Rosewood is very expensive and difficult to cut, since it tends to burn and collect on sawblade teeth, but its resonant qualities (i.e., low damping factor) cause it to "ring" much longer when struck. Therefore, its cost would seem to be justified in the better instruments. A "clean" knot-free portion of a large board must be selected, since all bars should be made from the same board so that the tone quality and appearance will be uniform. The moisture content of these wood bars will influence their elastic properties (and hence their pitch), so they will need to be sealed with a lacquer or varnish after final tuning. Possibly a moderate temperature bake-out prior to final tuning would help stabilize their pitch. An oven setting of 150 degrees for one hour is suggested, but some experimenting would be in order.

The tubular resonators under each bar on some instruments serve to amplify sound-especially the fundamental tone. These tubes are usually about equal in diameter to the width of the bars, and they are usually plugged at the end opposite the bar. They are acoustically analogous to a stoppered organ pipe, and they must be tuned by sliding the stopper inside the tube. Since the resonant pitch of the stoppered tube depends strongly on its proximity to the bar, It must be in final position before it is tuned. About 1/4 to 1/2 inch spacing is common. For rough tuning, the pitch of the resonator (independent of the bar) can be estimated by blowing into the tube, somewhat like "blowing across a bottle", and listening for the resulting tone. But be careful, since it is easy to err by exactly one octave in the estimation of pitch.

Many of these same principles apply in the construction and tuning of tubular chimes, and this subject will be covered in a forthcoming installment.

References:

1. "Elements of Acoustical Engineering", by Harry F. Olsen (Van Nostrand, 1949), page 52.
2. "Vibration and Sound", by Philip M. Morse (McGraw-Hill, 1948), page 154.
3. “Science of Percussion Instruments”, by Thomas D. Rossing (World Scientific Publishing Company, Inc., 2000, ISBN:9810241585), pp 64-67.
4. “The Physics of Musical Instruments”, by Neville H. Fletcher and Thomas D. Rossing (Springer-Verlag, 1998, ISBN 0-387-98374-0), Chapter 19. Mallet Percussion Instruments, pages 623-648.

About the author ...  Dr. Flynt is a physicist with Varo, Inc., Garland, Texas, in the field of night vision electro-optics (now retired), and holds the PhD degree in physics from the University of  Texas. He has built a 16 rank pipe organ for his church, where he has been organist for the past 12 years, and is otherwise involved in local musical activities. Only recently has he become interested in automatic musical instruments, and current projects include the development of a digital tape recording system for creating new reproducing piano arrangements from live performances, and several "drafting board" arrangements for the Ampico system.

In the late 1970s, he designed and built the digital electronic equipment which controls the operation of the perforating machines at Play-Rite Music Rolls in Turlock, California. This equipment is still in daily use at this time (January 2009).