| You Are Not Logged In | Login/Get New Account |
|
Please Log In. Accounts are free!
Logged In users are granted additional features including a more current version of the Archives and a simplified process for submitting articles. |
|
MMD
 Tech
Tech
 pouchforce
pouchforce
|
|
Pneumatic Pouch Forces - A Designer's Aid by Johan Liljencrants A pouch is a membrane used to actuate some device pneumatically, often one or more valve disks. Normally the pouch is made from thin leather, glued to the edge of a cylindrical well. The central part of the pouch is covered by a disk, either used directly as a valve or used as anchor for a valve stem. You apply a pressure difference P across the two sides of the pouch to actuate it. For the principle it is irrelevant whether you use pressure or suction, or lead the air to the well or to the other side of the pouch. The pressure difference results in a useful force F, acting to displace the central disk. This note describes in a qualitative way how that force depends of axial displacement D of the central disk and of the size of this disk compared to the well diameter.
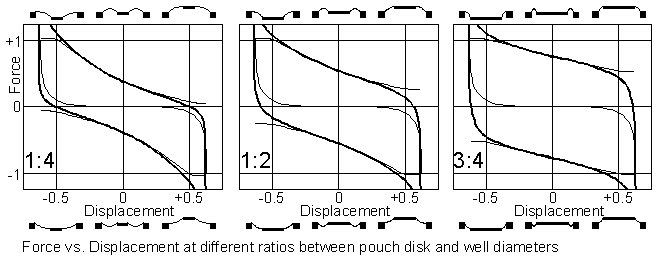
Let us define as nominal end positions of axial movement to be D=+0.5 and D=-0.5 where the bulge peak radius r equals the pouch disk and well radii respectively. Then D is the total nominal throw of the pouch. What this will be in mm or inches is determined by the amount of 'dish' installed by the builder when gluing the pouch in place. This also implies that maximum deflection, as a fraction of the pouch diameter, may be vastly different depending on what pouch material is used. Thin pouch leather would allow for a large throw, while e.g. the stiffness in a Mylar sheet would allow much less throw at the same well diameter. An additional parameter is how big the pouch disk is in relation to the well diameter. In the following diagrams three cases are shown where the ratio is 25, 50, and 75% respectively. With a small disk r and the resulting force diminish drastically as displacement approaches the end of the throw. Finally the pouch material itself will use some force to deform it, next to impossible to compute accurately. Here it is assumed that we use a flexible material that does not resist movements appreciably within the nominal displacement range. But beyond the end positions the pouch material will be stretched and the force to do that increases dramatically with displacement. The following diagrams show the parabolic curves for the pneumatic force, stylized S shaped curves for the pouch stretching force, and with heavy lines the resulting net force. All the diagrams show anti symmetrical cases, with operating pressure alternately applied to the two sides of the pouch. The indications of force are normalized. F=1 represents the force exerted by the operating pressure on the area of the pouch well. It should be noted that the available force in the usable displacement range is always smaller than that, sometimes very appreciably. When using a very soft pouch material it is possible to give much dish; the pouch is made so slack that it does a 'rollsock' movement in the middle range of travel. Then the bulge peak radius r is almost constant here, about midway between the well and disk radii and force is constant. The whole of this 'rollsock' range would be represented by D=0 in the diagrams. To ease interpretation little sketches of relevant pouch shapes are
shown above and below. The upper curves apply when the disk is blown upwards.
For instance, at the upper left corners is when we do that when the disk
is in its extreme low position (D= -0.5). In all cases the force
is then near 1, the nominal maximum. As we let the pouch disk travel upward,
going right in the diagrams, the force decreases as the critical radius
r
of the pouch moves. Similarly the lower curves and the small sketches below
apply when the pouch is blown downward.
These diagrams show the force generated by the pouch only and are intended
as a partial help in design. For a specific application you will additionally
have to specify what force and travel you need. In a valve application
you can for instance estimate the force necessary to operate the valve,
based on pressure and valve diameter. From the diagrams here you can compare
that requirement against the force the pouch can deliver.
DiscussionStarting from the upper left corner we could observe the difference between the three disk sizes. With the small disk (left diagram) the force decreases very much, when reaching the full upward position (D= +0.5) there remains essentially no force at all. With a big disk (right diagram) about half the original force is still available at the end of the throw. In general it would be better to select a bigger disk, right diagram. The drawback with this is that the maximum travel will be a comparatively small fraction of the pouch diameter. With a given pouch diameter a smaller disk will allow longer travel, but at the price of larger force variation.When disk movement is unrestricted, then the curve intersections with the F= 0 line tell the end positions of the disk blowing it down and up respectively. But in a normal application the movement is restricted, at least one way. Typical would be in a valve when the valve disk hits its seat(s), no matter if this disk is the pouch disk itself or a remote one connected by way of a stem. Then you would draw vertical lines in the diagrams representing those particular end displacements. In a block valve you might for instance allow the disk to move only between D= -0.2 and D= +0.2. Means you give the pouch enough dish to keep a margin - pouch stiffness and fabrication tolerances should not be allowed to impede action. It is of course not necessary that these limiting lines are symmetrically located on the displacement scales. It is common that you put a bias to the pouch force by inserting a spring. That spring force will then vary with displacement D, as determined by the spring stiffness (measured in e.g. N/m, gf/mm, lbf/in, or whatever). You should be warned that this is equivalent to increasing the slope in the curves here. The available force will then vary even more with displacement. When mounted, springs for that purpose are normally compressed to be several times shorter than when unmounted. The reason is you want to keep the spring force as constant as possible.
Johan Liljencrants 2001-07-26 |
|
|
|
|
|
|
|
|
|
CONTACT FORM: Click HERE to write to the editor, or to post a message about Mechanical Musical Instruments to the MMD Unless otherwise noted, all opinions are those of the individual authors and may not represent those of the editors. Compilation copyright 1995-2026 by Jody Kravitz. Please read our Republication Policy before copying information from or creating links to this web site. Click HERE to contact the webmaster regarding problems with the website. |
|
|
||||||
|
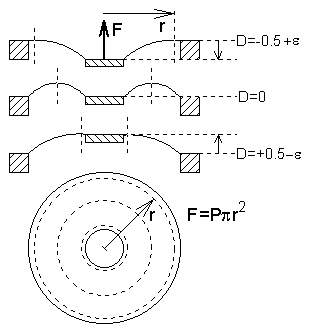 When
the well is pressurized the annular part of the pouch between the well
edge and the central disk will bulge. The precise cross section shape of
this bulge is complicated to compute but it is not far from circular. At
some radius r from the center of the pouch this bulge has its peak
or valley. At this place the tensional force in the pouch is purely radial.
The area of the pouch inside this radius will contribute to the pneumatically
induced useful force on the pouch disk, then being F=Ppr2.
Force on the remaining outside pouch area is unloaded against the well
edges and is of no use. This radius will vary, depending on the axial position
of the pouch disk. Again, precisely what it is is complicated to find out,
but with no appreciable error we can assume r to change in direct
proportion to axial position D. This means that the force will be
a parabolic function of D.
When
the well is pressurized the annular part of the pouch between the well
edge and the central disk will bulge. The precise cross section shape of
this bulge is complicated to compute but it is not far from circular. At
some radius r from the center of the pouch this bulge has its peak
or valley. At this place the tensional force in the pouch is purely radial.
The area of the pouch inside this radius will contribute to the pneumatically
induced useful force on the pouch disk, then being F=Ppr2.
Force on the remaining outside pouch area is unloaded against the well
edges and is of no use. This radius will vary, depending on the axial position
of the pouch disk. Again, precisely what it is is complicated to find out,
but with no appreciable error we can assume r to change in direct
proportion to axial position D. This means that the force will be
a parabolic function of D.